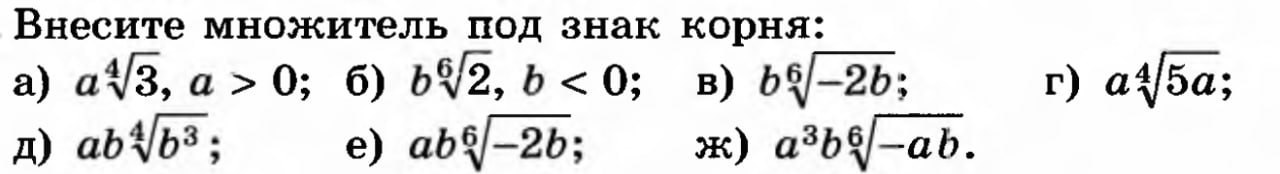Войти через telegram

Инструменты

Бот аналитики

Полезная информация

Инструкция Telemetr Документация к API Чат Telemetr

Полезные сервисы

Защита от накрутки Создать своего бота Продать/Купить канал Монетизация

Телеграм канал «Математика с нуля»

369

676

12

6

273

Геометрией он занялся поздно; кто-то спросил: «Разве теперь время для этого?» — «Неужели еще не время?» — переспросил Лакид.

По всем вопросам: @ederika
Чат канала: @marhfromzerochat
Наш Boosty: https://boosty.to/mathfromzero
Для помощи каналу: https://bo

Полная статистика канала

Подписчики

Всего

1 719

Сегодня

0

Просмотров на пост

Всего

243

ER

Общий

18.25%

Суточный

11.2%

Telemetr - сервис глубокой аналитики
телеграм-каналов

Получите подробную информацию о каждом канале

Отберите самые эффективные каналы для
рекламных размещений, по приросту подписчиков,
ER, количеству просмотров на пост и другим метрикам

Анализируйте рекламные посты
и креативы

Узнайте какие посты лучше сработали,
а какие хуже, даже если их давно удалили

Оценивайте эффективность тематики и контента

Узнайте, какую тематику лучше не рекламировать
на канале, а какая зайдет на ура

Попробовать бесплатно

Всего постов: 369

Смотреть все посты