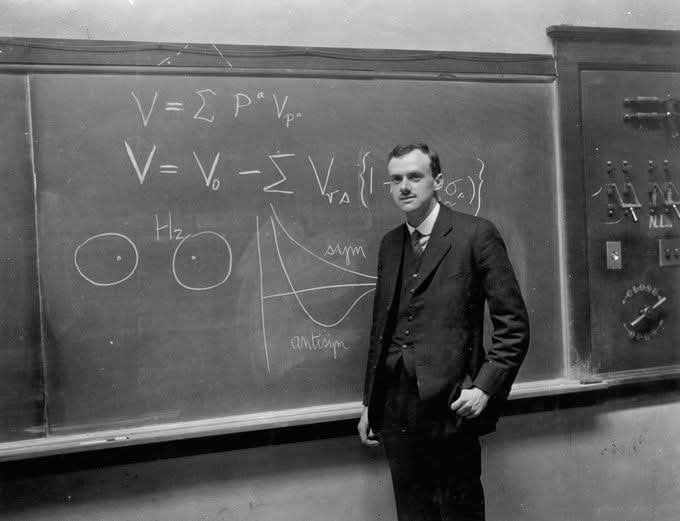Телеграм канал «Математика не для всех»
По рекламе: https://telega.in/c/mathematics_not_for_you и @andreybrylb

телеграм-каналов

рекламных размещений, по приросту подписчиков,
ER, количеству просмотров на пост и другим метрикам

и креативы
а какие хуже, даже если их давно удалили

на канале, а какая зайдет на ура

Новый сервер с 2 ТБ DDR5 стоит как 3 восстановленных с 4 ТБ DDR4 каждый.
Для виртуализации, 1С, K8s и критичных сервисов редко нужны новые поколения. Прирост производительности — 5-15%, а разница в цене — до 70%. Отказоустойчивый кластер часто лучше, чем один новый узел.
Наши восстановленные серверы — это не б/у с гарантией. Они прошли дефектоскопию, замену комплектующих (накопители — только новые), стресс-тесты и отбраковку. Даём гарантию 5 лет с выездом инженеров и держим свой склад ЗИП, чтобы снизить риски и ускорить сервис. Доставка по всей России — бесплатно.
Нужна консультация технического специалиста?
Обращайтесь — ответим на любые вопросы.
Сайт с чатом: servermall.ru
Телефон: 8 (800) 755-25-51
Узнать больше
#реклама
servermall.ru
О рекламодателе
Дирак никак не отреагировал и просто продолжил писать на доске. Через некоторое время студент решил, что Дирак его не услышал. Он повторил, уже громче: «Профессор Дирак, я не понимаю уравнение (2)».
Но реакции по-прежнему не последовало. Другой студент в первом ряду решил вмешаться. Он сказал: «Профессор Дирак, этот человек задает вопрос». Дирак помолчал, а потом ответил: «О, я думал, он делает заявление».
Вы когда-нибудь ловили себя на мысли: "я раньше так не думал"?
Есть старая притча: в деревне отравилась вода, люди начали сходить с ума, и даже мудрец в конце концов выпил из колодца - чтобы «быть как все».
Самое страшное там не яд. Самое страшное что он становится нормой.
Мы часто так и живём:
чуть устали - и начинаем верить любому шуму в голове.
чуть заболели - и мысли сразу темнеют.
чуть перегрузились - и уже кажется, что мир плохой, люди плохие, а жизнь «не про нас».
А ведь иногда достаточно одного вечера, чтобы снова стать трезвым внутри.
Не весёлым. Не «замотивированным».
А трезвым.
Записаться
#реклама 16+
opytduraka.online
О рекламодателе
Проект называется TUMIX, и, по мнению многих, это самая интересная работа Google в этом году.
💡 Вместо того чтобы обучать ещё одну гигантскую модель, команда Google построила систему, где несколько ИИ работают вместе во время инференса.
Каждый агент выполняет свою роль:
- один пишет код
- другой ищет информацию,
- третий рассуждает текстом.
Все они решают одну задачу независимо, затем обмениваются ответами, улучшают их и приходят к общему решению.
📈 Результат ошеломляющий:
Gemini 2.5 с TUMIX обошёл все другие системы рассуждения на +17,4%,
при этом стоимость инференса снизилась почти в два раза.
Без дополнительного обучения. Без новых данных. Просто - умная координация.
Самое неожиданное - секрет не в размере, а в разнообразии.
Команда из 15 разных агентов показала результаты лучше, чем 15 копий “лучшего” одиночного ИИ.
А когда Gemini сам спроектировал новых агентов, качество выросло ещё сильнее — система буквально эволюционировала сама себя.
🧠 Этот эксперимент показывает:
Следующий скачок в развитии ИИ может прийти не от триллиона параметров,а от сети маленьких моделей, которые учатся думать вместе.
✔️ Подробности: https://arxiv.org/pdf/2510.01279
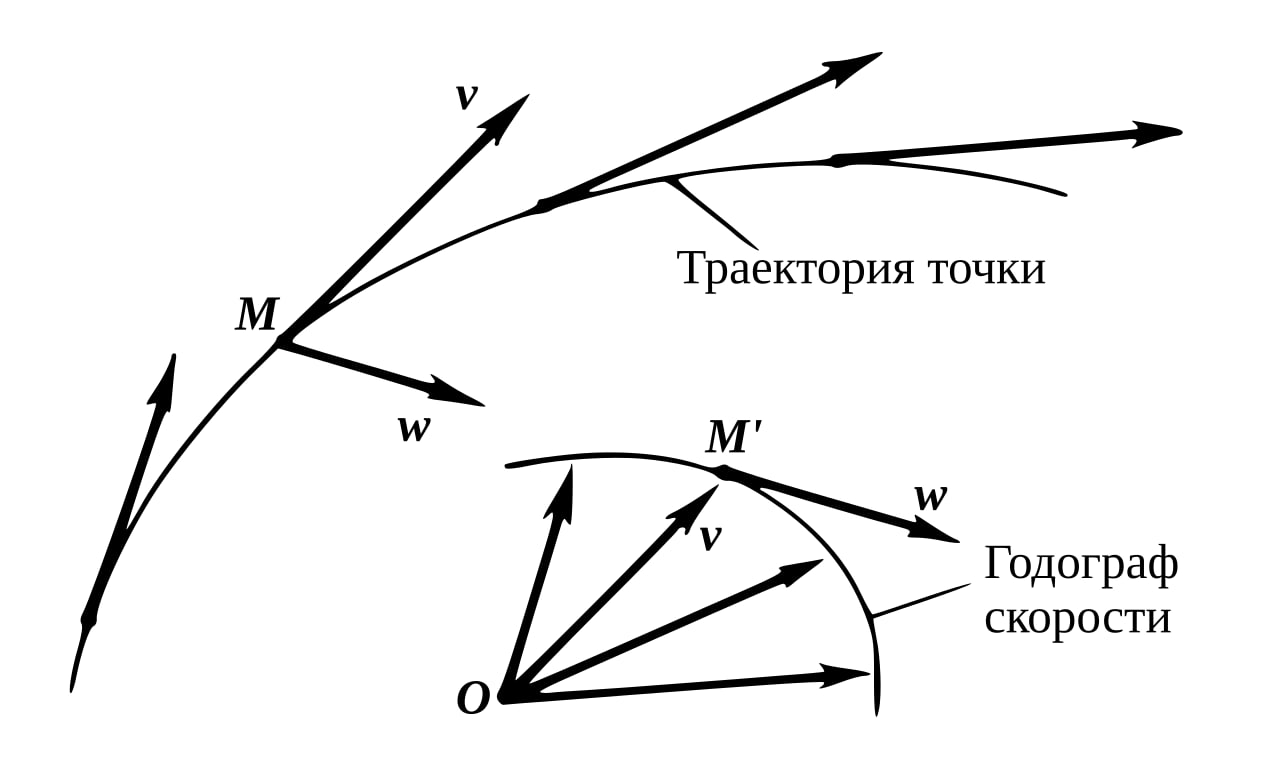
Но вот что особенно красиво в небесной механике: если вместо положения планеты начать следить за её скоростью, картина меняется самым неожиданным образом. Оказывается, вектор скорости — если откладывать его из начала координат во времени — описывает не эллипс, а идеальную окружность. И это верно даже тогда, когда сама орбита заметно вытянута.
Такую фигуру, которую «рисует» конец вектора скорости, называют годографом. Для круговой орбиты всё выглядит интуитивно: положение — круг, скорость — тоже круг с тем же центром. Но при эллиптическом движении происходит тонкость. Орбита остаётся эллипсом, а годограф всё равно оказывается окружностью, только её центр уже не совпадает с началом координат. Он смещён — и величина этого смещения напрямую связана с эксцентриситетом орбиты.
Если представить орбиту вытянутой вдоль оси x и поместить звезду в положительную область этой оси, то круг годографа будет смещён вверх. Чем более вытянут эллипс, тем сильнее это смещение. Верхняя точка окружности соответствует перигелию — моменту, когда планета ближе всего к звезде и её скорость максимальна. Нижняя точка отвечает афелию, где планета дальше всего и движется медленнее.
Музей математики под открытым небом «Математический парк» — вписанная в городское пространство коллекция арт-объектов, иллюстрирующих известные математические задачи и факты.
https://math-park.ru/ru/
https://urbanmediaasu.tilda.ws/
#math_in_culture
Думаете, что выбрать на 8 марта? Зачем выбирать, когда на Wildberries скидки до 60%.
Перейти на сайт
#реклама
wildberries.ru
О рекламодателе